
GAN은 현재 다른 방법보다 높은 품질의 샘플을 생성하지만 안정적인 훈련을 위해 feature 최적화와 architecture 선택이 필요하다. DDPN 및 NCSN과 같은 iterative generative model은 adversarial training 없이 GAN과 유사한 고품질 샘플을 생성할 수 있다. 그러나 이러한 모델은 단일 샘플을 생성하기 위해 여러 번의 반복이 필요하여 GAN보다 효율성이 떨어진다. 이러한 효율성 차이를 극복하기 위해 본 논문에서는 DDPM에서 사용되는 forward diffusion process을 일반화한 Denoising Distribution Implicit Model(DDIM)을 소개한다. DDIM은 non-Markovian diffusion process를 사용하며, 이를 통해 샘플 효율성을 증가시킬 수 있는 short generative Markov chain을 구현할 수 있다. 또한 본 논문에서는 DDIM이 DDPM보다 우수한 sample generation quality를 가지고 consistency property를 가지며 그렇기 때문에 meaningful image interpolation 수행할 수 있는 이점을 제시한다.

Figure 1: Graphical models for diffusion (left) and non-Markovian (right) inference models.
이 section에서는 DDPM에 쓰인 수식을 설명하고 있다.

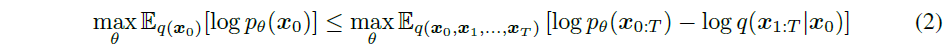
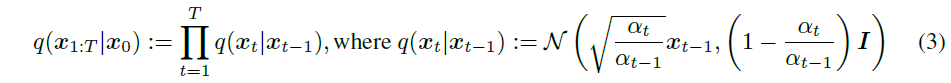
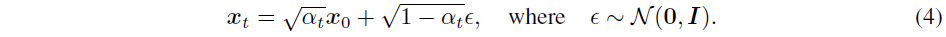
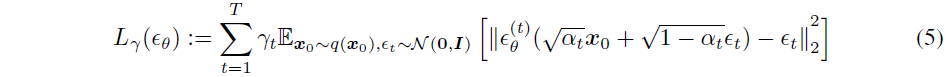
DDPM 논문에 있는 식과 살짝 다르다는 걸 확인할 수 있는데, 수식 전개의 편의성을 위해 DDPM 논문의 $\overline{\alpha}_t$를 본 논문에서는 $\alpha_t$로 표현하고 있다.
Non-Markovian인 경우 다음의 식이 성립한다. 여기서 각 확률분포 $q_\sigma$가 $\mathbf x_0$에 대한 conditional distribution이라는 점에 주목하자.
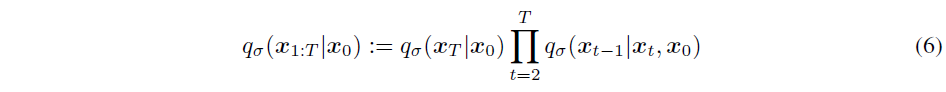
이때 Eq (4)에 의해 $q_\sigma (\mathbf{x}_T|\mathbf{x}_0) = \mathcal{N}(\sqrt{\alpha_T} \mathbf{x}0, (1-\alpha_T)\mathbf{I})$이고, 이를 이용하면 $\mathbf{x}{t-1}$을 $\mathbf{x}_t$와 $\mathbf{x}_0$로 다음과 같이 나타낼 수 있다. 이 과정에서 reparameterization trick이 사용되었다.
$$ \begin{align*} \mathbf{x}{t-1} &= \sqrt{\alpha{t-1}} \mathbf{x}0 + \sqrt{1-\alpha{t-1}} \epsilon_{t-1} \\ &= \sqrt{\alpha_{t-1}} \mathbf{x}0 + \sqrt{1-\alpha{t-1}-\sigma_t^2} \epsilon_t + \sigma_t \epsilon \\ &= \sqrt{\alpha_{t-1}} \mathbf{x}0 + \sqrt{1-\alpha{t-1}-\sigma_t^2} \cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_0}{\sqrt{1-\alpha_t}} + \sigma_t \epsilon \end{align*} $$